UN MODELO MATEMATICO PARA ENCUESTAS PRESIDENCIALES

Un Modelo Matemático para Encuestas Presidenciales

Introducción: Ya que en este año de elección presidencial en México llueven encuestas por doquier, hablemos del modelo matemático que justifica, bajo ciertas condiciones, la efectividad de una encuesta.

Desarrollo:

¿Qué es un modelo matemático? Digamos que es una maqueta de una situación real que se construye con conceptos y lenguaje matemático para plantear y resolver un problema.

 
Un modelo matemático es uno de los tipos de modelos científicos que emplea algún tipo de formulismo matemático para expresar relaciones, proposiciones sustantivas de hechos, variables, parámetros, entidades y relaciones entre variables y/o entidades u operaciones, para estudiar comportamientos de sistemas complejos ante situaciones difíciles de observar en la realidad.

Una maqueta necesariamente simplifica o reduce la realidad, tratando de mantener la esencia de lo que queremos plantear y resolver.

¿Y qué es una encuesta?

En principio es un instrumento para sondear la realidad en un momento determinado.

Una encuesta es un estudio observacional en el cual el investigador busca recaudar datos de información por medio de un cuestionario prediseñado, y no modifica el entorno ni controla el proceso que está en observación (como sí lo hace en un experimento).
En este caso quisiéramos conocer la intención de voto de los mexicanos con posibilidad de votar el próximo 1° de julio. Pensemos pues en un conjunto de 90 millones de puntos encerrados en una región, digamos un cuadrado.
Cada punto está pintado de un color, que puede ser azul, rojo, amarillo o blanco. En esta maqueta, el cuadrado representa el territorio nacional, los puntos representan a los mexicanos en la lista nominal del IFE (para simplificar estamos excluyendo los mexicanos votantes en el extranjero), y los colores representan la intención de votar, respectivamente, por los candidatos presidenciales, JVM, EPN, AMLO, o dejar en blanco su voto.
También para simplificar, supongamos que los puntos del cuadrado están distribuidos uniformemente, es decir que en cualquier parte del cuadrado hay la misma densidad de población. En nuestro modelo matemático, una encuesta consiste en considerar un subconjunto de puntos, de mucho menor tamaño, digamos 900 puntos (es decir, una cienmilésima parte del conjunto original). Este subconjunto representa lo que los encuestadores llaman muestra. Para que esta muestra sea ideal, la proporción numérica de los colores debe ser igual (o acercarse lo más posible) a la proporción de colores en el conjunto original.
El problema matemático consiste en encontrar dicha muestra ideal.
La respuesta es que para reflejar la realidad de manera precisa, la encuesta debe aplicarse al azar, es decir, la muestra debe ser aleatoria.

Esto se traduce en que los 900 puntos elegidos aparezcan distribuidos uniformemente dentro del cuadrado original. Para garantizar esta repartición uniforme de la muestra, podemos pensar en cuadricular la región, digamos que formando 900 cuadritos (subdividiendo el lado del cuadrado original en 30 segmentos), lo cual significa que cada cuadrito tiene el mismo número de puntos (en este caso 100 000), y luego elegir un punto de cada cuadrito. Bajo estas condiciones, en efecto la proporción de los colores de la muestra es cercana a la proporción de estos en el cuadrado original. ¿Cómo se tiene la certeza de esto? Con el concepto matemático de probabilidad.
La probabilidad de que al elegir al azar un punto de la muestra sea, digamos, amarillo, se acerca al porcentaje de puntos amarillos de la muestra. Este acercamiento es mayor mientras más puntos tiene la muestra, pero 900 puntos son suficientes para un buen acercamiento. Dicha probabilidad se puede calcular de manera precisa, y resulta que bajo las condiciones descritas coincide con el porcentaje real de puntos amarillos en el conjunto original.

En conclusión, si la muestra se conforma de esa manera, subdividiendo el conjunto original en pedazos con el mismo número de puntos, y eligiendo al azar un punto en cada uno de esos pedazos, los porcentajes de colores en la muestra serán muy cercanos a los porcentajes reales. Si la muestra no se construye así, no hay garantía de que se dé este acercamiento.

Regresemos a la compleja realidad. Según nuestro modelo matemático, para garantizar que la muestra sea aleatoria, y por tanto que la encuesta sea efectiva, hay que subdividir la población de votantes en pedazos con el mismo número de votantes y luego elegir al azar una persona de cada pedazo para aplicarle la encuesta. En la medida en que estas dos condiciones se cumplan, la encuesta será efectiva.

Por supuesto hay dificultades reales para llevar a cabo esto. O bien, puede tenerse la intención de que dichas condiciones no se cumplan, y en tal caso la encuesta se realiza con el objetivo de tener un resultado favorable a alguno de los candidatos.

Esto explica el hecho de que distintas encuestas ofrecen distintos resultados. Si todas se aplicaran con las mismas condiciones, la certeza matemática nos llevaría al mismo resultado inequívoco. Idealmente, al informar los resultados de cada encuesta se debería incluir también con detalle la manera como se eligió la muestra, es decir, cómo se hicieron las subdivisiones y luego cómo se garantizó la aleatoriedad de la elección de cada persona.

De otra manera, creer en una encuesta se convierte en un dogma de fe, con la posibilidad de ser utilizado de manera mal intencionado para inducir el voto.

Estudio matemático pronostica que Andrés Manuel López Obrador ganaría las elecciones presidenciales

Nota: El siguiente análisis realizado por el Investigador de la U.V., Gerardo Ortigoza Capetillo, es eso, un análisis, no significa que la gente se deba confiar y dejar de ir a votar y cuidar las casillas. Pienso que por el contrario, hay muchas posibilidades para que vuelvan a hacer un fraude electoral por lo que hay que salir a votar y aumentar el porcentaje con el que pueda ganar López Obrador.

AMLO ganaría con 37.96% del voto y EPN quedaría en segundo lugar con 30%, señala el estudio.

Ciudad de México – Un estudio matemático predice que Andrés Manuel López Obrador ganaría las elecciones presidenciales del primero de julio.

Los resultados que arroja el estudio indican que AMLO ganaría con 37.96%, Enrique Peña Nieto quedaría en segundo lugar con 30.7% y Josefina Vázquez Mota en tercero con 27.93%. Esto debido a que los priistas, sugiere el estudio, realmente no están dispuestos a promover a Peña Nieto por su propia iniciativa.

El estudio fue hecho por Gerardo Ortigoza Capetillo, profesor investigador en la facultad de Ingenierìa Universidad Veracruzana, quien tiene además un doctorado en matemáticas aplicadas por la University of Minnesota.

De acuerdo con el estudio, la evolución en el tiempo de la intención de voto en México arroja resultados favorables a López Obrador.

“Este modelo probó su efectividad en 2009, pues predijo un resultado muy cercano al resultado oficial en la elección de diputados del distrito 4 Veracruz Boca del Rio. La encuesta Mitofsky daba un 38.8% al rojo y un 29.8% al azul. En esa ocasión el modelo arrojó victoria roja con 41.02% sobre 40.15% del azul (una diferencia de 0.87% ), mientras que los resultados oficiales fueron victoria roja con 43.86% sobre azul con 43.28 % (una diferencia de 0-58% )”, señala el estudio.

“El modelo de autómata celular utiliza el total de la lista nominal, cada ciudadano es considerado como un elemento de una retícula, la intención de voto de cada ciudadano se ve influenciada por el círculo social a su alrededor: familiares, vecinos, amigos, compañeros de trabajo, etc”, continúa la descripción del estudio.

“Consideramos tres partidos: amarillo, rojo y azul, así como indecisos. Identificamos tres tipos de votantes en cada partido: el voto duro, el voto normal y el voto blando. El voto duro son personas que votan por su partido, hacen promoción del voto y además tienen una posición dentro de su partido; el voto normal vota por su partido hace promoción pero no tiene una posición dentro del partido; finalmente el voto blando solo se concreta a vota por su partido.

“Las suposiciones básicas del modelo son que cada partido es capaz de mantener su voto duro (el total de la elección anterior), el voto normal se estima mediante la razón de crecimiento proporcionado por el historial de datos. Para estimar el voto blando se usó la encuesta Covarrubias que otorga al rojo 36.84%, 26.36% al amarillo y 23.69 % al azul. Asumimos un 60% de participación ciudadana en la jornada electoral”, indica.

El estudio explica:

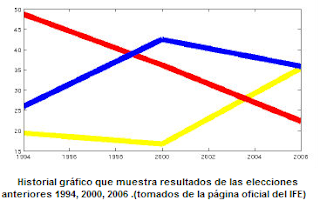
La gráfica del historial nos muestra una clara tendencia a la baja del rojo, amarillo viene de abajo creciendo mientras azul comienza declive. Cuantificamos los datos iniciales clasificando el tipo de voto para obtener lo que serían los datos iniciales del código:

Amarillo: duro 12,091,475, normal 815,006, blando 0.

Rojo: duro 9,301,441, normal 0, blando 8061831

Azul: duro 9,604,292, normal 1,561,178 blando 0

Las observaciones inmediatas de esta cuantificación de datos, es que el voto del rojo dividido quedando gran parte de él muy debilitado pues el voto blando fácilmente se pierde. El hecho de que el voto normal rojo se haya cuantificado a cero explica políticamente que los rojos se sienten avergonzados y no participan activamente promoviendo voto rojo, aun así votan rojo pero tratan de refugiarse en una coalición por ejemplo el partido verde. Los votos blandos cero en azul y amarillo pueden políticamente explicarse ya que por una parte la guerra sucia del 2006 que afectó al amarillo asi como la incertidumbre de un posible fraude electoral del 2006 que afecta al azul. Se implementó un código en C++. Y se ejecutó en una workstation con ubuntu linux. Con estos datos de entrada se simuló a 90 días, promediando los resultados de las simulaciones se obtiene que el amarillo obtendrá la victoria con 37.96%, sobre el rojo con 30.7% y azul 27.93%.

Según el autor: el método identifica el comportamiento del elector en grupos, y como cada elector decide su voto en base a decisiones de grupo.

“Psicológicamente una persona se siente influenciada por su circulo social  y tiende a se afín con la mayoría. En política se le conoce también como “cargada”, ya que todos quieren estar con el ganador y nadie quiere apoyar al perdedor”

El modelo matemático desarrollado mide precisamente el efecto del entorno del votante en su preferencia electoral.

Y tiene sentido. Hace un año, todo el mundo pensaba que Enrique Peña Nieto seria el ganador en las elecciones, y su preferencia electoral estaba supuestamente arriba de 50%. Es decir, como todos creían que Peña ganaría, todos decían que iban a votar por el. 

Pero conforme la gente fue dándose cuenta de que Peña es un ignorante y un represor, su preferencia electoral se ha desplomado.

Precisamente por eso es que Peña Nieto y el PRI prendieron focos rojos con las protestas de la Ibero. Porque la tendencia de varios entornos sociales donde el PRI encontraría su principal apoyo se convirtió en una tendencia en CONTRA de Peña Nieto.

Y como ya se ha explicado, la cultura viral de los jóvenes, que tiene como principal media de comunicación a las redes sociales, prácticamente garantiza que el rechazo a Peña nieto se propague de manera acelerada y exponencial entre el electorado que el PRI suponía que iba a ser su principal fuente de votos: la clase media.

Y pregúntenles por quién van a votar entonces y muy probablemente le van a responder que le van a dar el beneficio de la duda al Peje.

Conclusión: la veracidad de las encuestas en nuestro país esta siendo cuestionada con gran severidad ya que muestran información incierta cosa que en lo particular me he encontrado, ejemplo siendo apartidista y usuario activo de las redes sociales mi pregunta es quien votaría por el PRI y hasta ahora no conozco a alguna persona que si votaría por ellos, mi duda es como en las encuestas sale que el PRI va a la cabeza! Pues a quienes encuestan y de donde???

www.blogdeizquierda.com

revistaemet.com

pocamadrenews.wordpress com

wikipedia